Abstract
Adversarial process를 통해 generative model을 훈련하는 GAN을 제안하였다. 이 훈련의 framework는 generator G와 discriminator D의 minimax게임이다. 이론적으로 optimal한 경우에는 G는 training data distribution과 동일한 분포의 데이터를 만들어내고 이 상황에서 D는 1/2를 내뱉어야한다. 구현상으로 G,D는 MLP로 구성되며 backprop으로 학습된다. 그리고 Markov Chain과 unrolled approximate infeerence netowrks가 training이나 generation of samples 과정에서 사용하지 않아도 된다. 실험을 통해 GAN으로 생성된 이미지의 정량,정성적 결과를 보여준다.
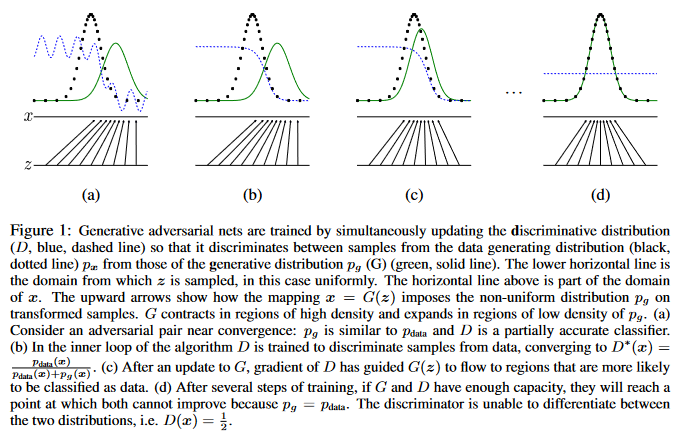
Adversarial nets
\[\min_{G} \max_{D} V(D,G)=\mathbb{E}_{x\sim p_{\text{data}}(x)}[\log D(x)] + \mathbb{E}_{z\sim p_z(z)}[\log D(G(z))]\]Experiments
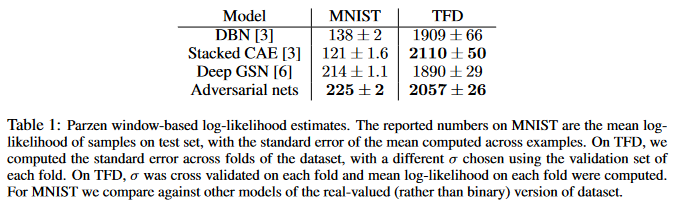

- MNIST, Toronto Face Database(TFD), CIFAR-10으로 훈련
- Gaussian Parzen window로 생성된 이미지들에 대한 log-likelihood를 추정하여 비교하였다.(현재는 잘 안하는듯.., variance가 크다..)
Advantages and disadvantages
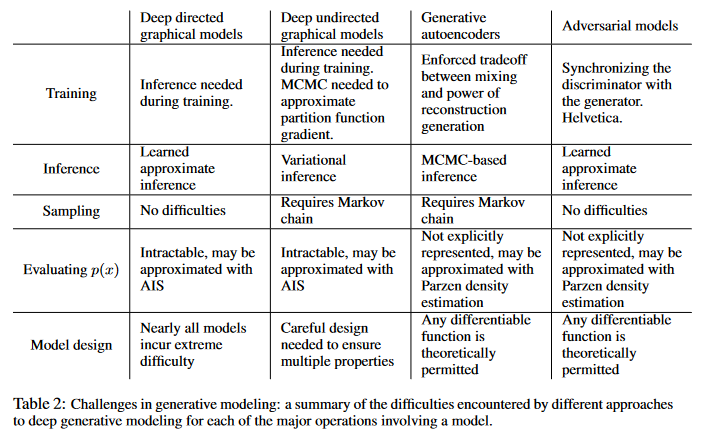
Pros
- 장점은 Markov Chain이 전혀 필요하지 않고 훈련시 backprop만 하면 된다. 그리고 $G$를 만들때 자유도가 있다.(MLP덕분)
- 통계적 장점도 가진다. Generator $G$가 훈련될 때 sample $x$에 의해 직접적으로 backprop이 진행된다기 보다, discriminator를 통해서 gradient가 간접적으로 update되기 때문에 sample에 overfit되는 현상을 어느정도 막아줄거라고 볼 수 있다.
- 또한 VAE나 Markov chain이 필요한 생성모델 과는 다르게 굉장히 “sharp”한 이미지가 생성되는 것을 정성적으로 확인할 수 있다.
Cons
- 단점으로는 generative model로부터 생성되는(sampling되는) $p_g(x)$의 정확한 식(formula)을 explicit하게 나타내지 못한다는 것이다.
- 또한 Discriminator $D$가 minimax 게임 도중에 “잘 훈련”이 되어야 된다는 것이다.(만일 그렇지 않고, Generator $G$만 훈련이 과도하게 되면 너무 많은 과도한 $z$값이 “하나의 $x$로만 대응되도록 훈련되어 문제가 생긴다.)
Conclusion
다음의 extension이 가능하다고 한다.
- 어떤 조건 $c$를 추가하여 조건부 생성 모델 $p(x\lvert c)$를 만들어 낼 수도 있다.(이게 아마 InfoGAN? ㄷㄷ)
- Learned approximate inference: GAN을 훈련한 다음에 혹은 훈련 도중 추가 network를 도입하여 $x$에 대응하는 $z$를 찾는 모델도 만들 수 있다.
- 뭔지 모르겠다..
-
One can approximately model all conditionals p(xS x6 S ) where S is a subset of the indices of x by training a family of conditional models that share parameters. Essentially, one can use adversarial nets to implement a stochastic extension of the deterministic MP-DBM.
- Semi-supervised learning: features from teh discriminator or inference net이 사용될 수 있다.
- Efficiency improvements: G,D의 model을 좀 더 잘 만들거나, $z$의 분포를 좀 더 잘 사용하면 더 나은 결과가 나올 수도 있다.
If you like this post, don’t forget to give me a star. ![]()
